Nonlinear acoustics

Non-linear acoustics is a branch of physics dealing with sound waves being distorted as they travel.

1 Introduction
2 Physical Analysis
3 Mathematical model
4 Common occurrences
5 References

Introduction

A sound wave propagates through a material as a localized pressure change. Increasing the pressure of a gas increases its temperature and the speed of sound in a compressible material increases with temperature; as a result, the wave travels faster during the high pressure phase of the oscillation than during the lower pressure phase. This affects the wave's frequency structure; for example, in a plane sinusoidal wave of a single frequency, the peaks of the wave travel faster than the troughs, and the signal becomes more like a sawtooth wave. In doing so, other frequency components are introduced, which can be described by the Fourier Series. This phenomenon is characteristic of a non-linear system, since a linear acoustic system responds only to the driving frequency.

Additionally, waves of different amplitudes will generate different pressure gradients, contributing to the non-linear effect.

Physical Analysis

The pressure changes within a medium cause the wave energy to transfer to higher harmonics. Since attenuation generally increases with frequency, a counter effect exists that changes the nature of the nonlinear effect over distance. To describe their level of nonlinearity, materials can be given a nonlinearity parameter, 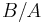$B/A$ . The values of $A$ and $B$ are the coefficients of the first and second order terms of the Taylor series expansion of the equation relating the material's pressure to its density. Typical values for the nonlinearity parameter in biological mediums are shown in the following table.^[1]

Material	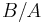$B/A$
Blood	6.1
Brain	6.6
Fat	10
Liver	6.8
Muscle	7.4
Water	5.2

Mathematical model

The propagation of sound beams in a medium that exhibits non-linearity, diffraction and absorption is described by the Khokhlov-Zabolotskaya-Kuznetsov (KZK) equation.^[2] Solutions to this equation are generally used to model non-linear acoustics.

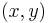If the $z$ axis is in the direction of the sound beam path and the $(x,y)$ plane is perpendicular to that, the KZK equation can be written^[3]

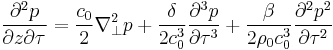
$\, \frac{\partial^2 p}{\partial z \partial \tau} = \frac{c_0}{2}\nabla^2_{\perp}p %2B \frac{\delta}{2c^3_0}\frac{\partial^3 p}{\partial \tau^3} %2B \frac{\beta}{2\rho_0 c^3_0}\frac{\partial^2 p^2}{\partial \tau^2}$

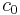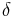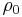where $p$ is the sound pressure, $c_0$ is the small signal sound speed, $\delta$ is the sound diffusivity, $\beta$ is the non-linearity coefficient, $\rho_0$ is the ambient density and 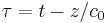$\tau = t-z/c_0$ is retarded time.

The equation can be solved for a particular system using a finite difference scheme. Such solutions show how the sound beam distorts as it passes through a non-linear medium.

Common occurrences

Sonic boom

The nonlinear behavior of the atmosphere leads to change of the wave shape in a sonic boom. Generally, this makes the boom more 'sharp' or sudden, as the high-amplitude peak moves to the wavefront.

Acoustic levitation

The practice of acoustic levitation would not be possible without understanding nonlinear acoustic phenomena.^[4] The nonlinear effects are particular evident due to the high-powered acoustic waves involved.

Ultrasonic waves

Because of their relatively high amplitude to wavelength ratio, ultrasonic waves commonly display nonlinear propagation behavior. For example, nonlinear acoustics is a field of interest for medical ultrasonography because it can be exploited to produce a better image quality.

References

^ Ultrasonic imaging of the human body, P N T Wells, Rep. Prog. Phys
^ Anna Rozanova-Pierrat (PDF). Mathematical analysis of Khokhlov-Zabolotskaya-Kuznetsov (KZK) equation. Laboratoire Jacques-Louis Lions, Université Pierre et Marie Curie. http://hal.archives-ouvertes.fr/docs/00/11/21/47/PDF/R06022.pdf. Retrieved 2008-11-10.
^ V. F. Humphrey (PDF). Non-linear propagation for medical imaging. Department of Physics, University of Bath, Bath, UK. http://www.sfa.asso.fr/wcu2003/procs/cd1/articles/000383.pdf. Retrieved 2008-11-10.
^ http://science.howstuffworks.com/acoustic-levitation.htm